Handwerker verstehen mit Data Science
This post is also available in English. Click here to download.
Die digitale Verarbeitung und das maschinelle Verstehen von Handwerkerrechnungen sind eine ernstzunehmende Herausforderung. Es ist der erste Schritt auf dem Weg, Maschinen beizubringen, Texte so zu lesen und zu verarbeiten, wie wir Menschen es können. Worte verstehen zu können, bedeutet für Computer, diese in Zahlen und Vektoren abzubilden. Die ausgereiftesten Methoden des Maschinenlernens (z.B. GloVe, Word2Vec oder fasttext) ermöglichen es, Wortvektoren aus unstrukturierten Textdaten zu erlernen. Diese Vektoren (auch als Worteinbettungen bezeichnet) erlauben es Maschinen, dem menschlichen Verständnis von Sprache zu folgen, indem sie Wörter nach semantischen Ähnlichkeiten gruppieren und analysieren.
Auswertungen von Rechnungen ist eine menschliche Stärke
Allein in Deutschland wurden 2016 über 22 Millionen Sachschäden bei Versicherungen gemeldet. Deren Bearbeitung bedeutet, dass über 30 Millionen Rechnungen und Angebote ausgewertet werden mussten. sachcontrol geht neue Wege, um diesen Prozess zu optimieren – mit dem Einsatz von Data Science und Big Data Methoden.
Bis heute gibt es in Deutschland noch keine einheitlichen Standards oder festgelegten Formate für Handwerkerrechnungen. Üblicherweise verwenden die Handwerker beim Erstellen dieser Dokumente unterschiedliche und persönlich geprägte Ausdrucksformen, um die Tätigkeiten und die für die Arbeiten benötigten Materialien zu beschreiben. Mitunter fehlen auch für die Prüfung der Belege wichtige Angaben in den Unterlagen. Für Laien sind die Texte in der Regel nicht nachvollziehbar. Daher bedarf es Expertenwissen und ein tiefgreifendes Verständnis für die Bausteine, aus denen eine Rechnung aufgebaut ist, und deren Zusammenhänge, um Belege vollumfänglich zu begreifen. Ein Experte würde angesichts der Unüblichkeit sofort zweifelnd die Augenbrauen heben, wenn für den Austausch von 5m² Fliesen 16 Arbeitsstunden veranschlagt wären. Dem Laien hingegen würden die überhöhten Arbeitswerte mitunter entgehen.
Heutzutage braucht es Experten mit menschlicher Intelligenz, um Handwerkerbelege zu verstehen. Dabei böte der Einsatz maschineller Prozesse zur Unterstützung der Prüfung offensichtliche Vorteile für Versicherungen und Geschädigte: höhere Kosteneffizienz, schnellere Bearbeitungszeit, verringerte Fehlerquote. Doch der Weg, Computern das Verstehen von Handwerkerrechnungen zu ermöglichen, ist noch holprig. Der erste Schritt dahin ist es, Maschinen beizubringen, natürlich gesprochene Sprache, die der Handwerker in seinen Dokumenten verwendet, zu verarbeiten.
Vektordarstellung von Worten
Anders als Menschen können Computer sehr gut mit Zahlen umgehen, aber nicht mit Worten. Um diese Schwachstelle auszugleichen, müssen Wörter in Zahlen umformatiert werden. Der naive Ansatz wäre, alle möglichen Wörter unserer Sprache zu zählen und jedem Wort eine Zahl zuzuordnen. Diese Methode wäre einfach umzusetzen und würde es Computern erlauben, Wörter voneinander zu unterscheiden. Sie hat jedoch auch einen ganz entscheidenden Nachteil. Die fortlaufende Nummerierung von Worten würde nichts über die Beziehung zwischen diesen aussagen. Computer wären somit nicht in der Lage, Ähnlichkeiten zwischen Wörtern und deren Eigenschaften zu bestimmen.
Ein natürlicherer und effizienterer Ansatz, um dieser Thematik Herr zu werden, ist, Wörter vieldimensionalen Vektoren zuzuordnen. Durch diese Vektoren können Ähnlichkeiten und Unterschiede zwischen Wörtern veranschaulicht werden. Um genau zu sein: Werden Wörter vektorisiert, dann verkleinern sich die Abstände zwischen den Vektoren, wenn sich Worte ähnlich sind. Bei Worten, die nichts miteinander zu tun haben, sind die Abstände größer. Das lässt sich an folgendem Beispiel besser verdeutlichen.
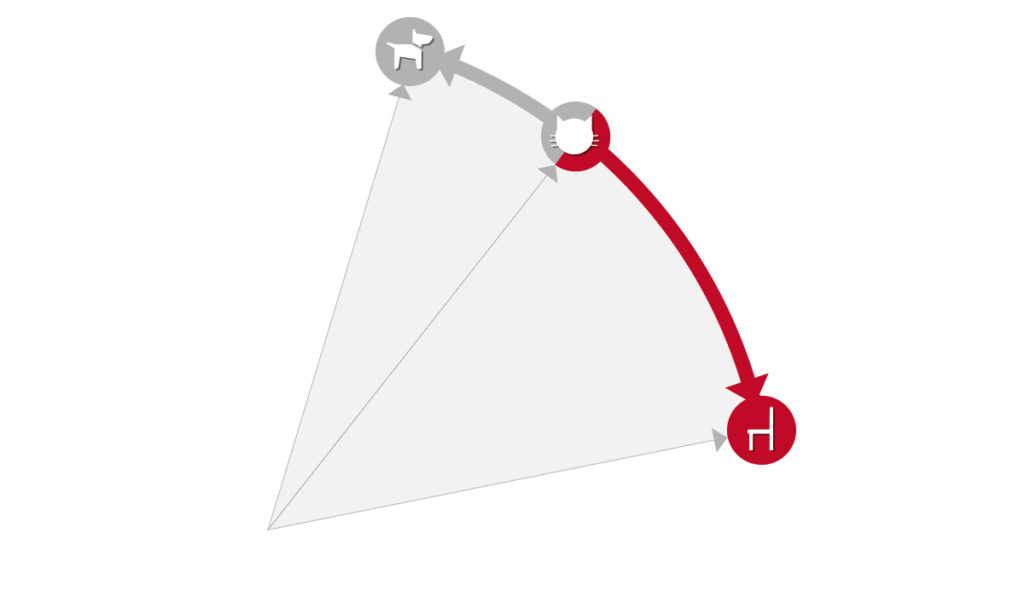
Ein Mensch wird intuitiv sofort zustimmen, dass das Wort „Katze“ mehr Gemeinsamkeiten mit dem Wort „Hund“ aufweist, als mit dem Wort „Stuhl“. Diese menschliche Intuition wird einem Computer dadurch verständlich gemacht, dass der Abstand zwischen „Katze“ und „Hund“ in einer vektorisierten Darstellung deutlich kleiner ist, als der Abstand zwischen „Katze“ und „Stuhl“. In einer stark vereinfachten Darstellung würde das in etwa so aussehen:
Leider kann das menschliche Gehirn nur drei Dimensionen visuell verarbeiten. Daher ist es für uns – besonders wenn man nicht Mathematik studiert hat – schwer greifbar, dass der tatsächliche Vektorraum nicht nur drei Dimensionen hat, sondern mehrere Hundert oder sogar Tausend.
Bei dieser Methode der vektorisierten Verdichtung von Wörtern bedarf es einem Weg, jedem Wort einen solchen Vektor zuzuordnen. Diesen Prozess manuell abzuarbeiten und alle Beziehungen zwischen Wörtern einer Sprache so festzustellen ist sehr unpraktisch. Glücklicherweise können Maschinen diesen Prozess selber lernen – von der Art und Weise, wie Menschen Wörter in geschriebenen Sätzen verwenden.
Wortverbindungen lernen
Effiziente Methoden, um die Verbindungen zwischen Wörtern zu lernen, basieren auf der Beobachtung, dass Wörter, die ähnliche Bedeutungen haben, häufiger in Sätzen natürlicher geschriebener Sprache in gleichem Kontext auftauchen. Synonyme zum Beispiel können daran erkannt werden, dass sie in identischen Satzkonstruktionen verwendet werden. Die Bedeutung von und Beziehung zwischen Wörtern lernt der Computer also nicht von den Wörtern selber, sondern von welchen anderen Wörtern diese häufig umgeben sind. Diese Methode ähnelt dem Vorgehen, das Menschen beim Erlernen einer Fremdsprache anwenden, wenn sie anstatt die direkte Übersetzung eines Wortes im Wörterbuch nachzuschlagen, das entsprechende Wort direkt in der Fremdsprache umschreiben.
Es ist wichtig zu erkennen, dass Objekte, die mit Wörtern beschrieben werden, sehr vielschichtig sein können. Jedes Objekt besitzt eine Reihe von Eigenschaften (Farbe, Form, Gewicht etc.). Außerdem kann jedes Objekt mit mehreren Tätigkeiten kombiniert werden (bewegen, streichen, heben, genießen etc.). Alle diese verschiedenen Aspekte eines Wortes lernen Computer aus dem Kontext, in dem das Wort auftritt und definieren die multidimensionalen Vektoren, die das Wort repräsentieren. Obwohl es nicht in jedem Fall möglich ist, einer bestimmten Dimension des Vektors eine genaue Bedeutung zuzuweisen, so gilt im Allgemeinen doch: Je näher sich die Vektoren von Wörtern sind, desto mehr Gemeinsamkeiten haben diese Wörter.
Beispiel: Das Wort „Laminat“ hat viele Gemeinsamkeiten mit dem Wort „Parkett“, was auch leicht nachvollziehbar ist. Basierend auf der Tatsache, dass sprachliche Bezeichnung für Reparaturwege gleich sein können, hat „Laminat“ aber auch gewisse Übereinstimmungen mit den Wörtern „Türrahmen“ und „Spülbecken“ und taucht daher in Rechnungstexten häufig in ähnlichem Zusammenhang auf.
Vektoren verstehen
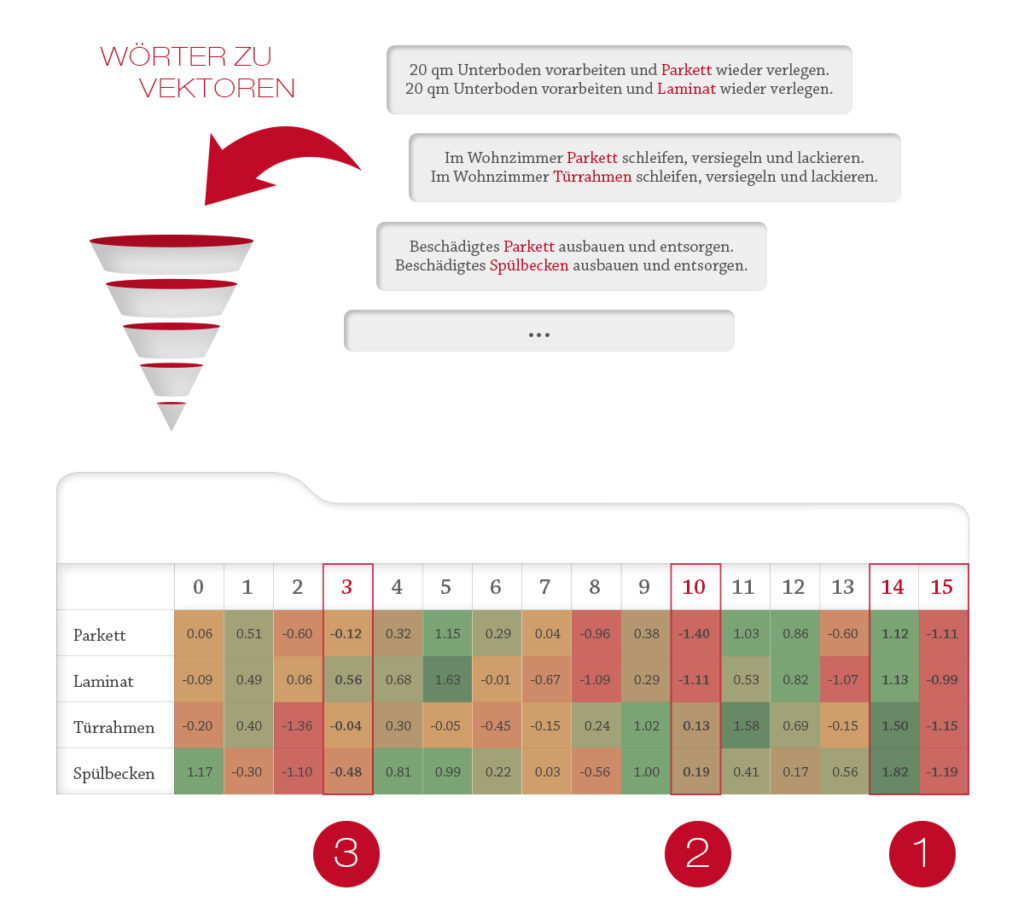
Verschiedene semantische Eigenschaften werden in Zahlenwerte umgewandelt, um den Vektor zu erstellen. Diese haben häufig mehrere hundert Dimensionen. Das folgende Beispiel verwendet zur Veranschaulichung eine Reduktion auf 16 Dimensionen (16D). Es ist nicht immer möglich oder technisch notwendig, den einzelnen Komponenten der Vektoren für den Menschen verständliche Bedeutungen zuzuordnen. Um jedoch ein grundlegendes Verständnis des Verfahrens zu erlangen, habe ich es in dem nachfolgenden Beispiel versucht.
Wir nehmen an, dass die Vektorkomponenten 14 und 15 (1) einige semantische Eigenschaften beschreiben, die alle vier Begriffe Parkett, Laminat, Türrahmen und Spülbecken gemeinsam haben – zum Beispiel, dass es sich bei allen Begriffen um Teile am Haus handelt, die in Zusammenhang mit gleichen weiteren Textbestandteilen auftreten können (Schaden, reparieren, austauschen, Versicherung). Die Vektorkomponente 10 (2) stellt eine Eigenschaft dar, die aufzeigt, dass es starke Ähnlichkeiten zwischen „Laminat“ und „Parkett “ sowie zwischen „Türrahmen“ und „Spülbecken“ gibt. Es zeigt aber auch, dass die Paare untereinander sehr unterschiedlich sind. Das könnte daher stammen, dass „Laminat“ und „Parkett“ Bodenbeläge sind, während „Türrahmen“ und „Spülbecken“ an Wänden angebracht werden. Komponente 3 des Vektors (3), die sich als ziemlich unterschiedlich zwischen allen vier Begriffen darstellt, könnte sich auf die Materialen und Methoden bei deren Reparatur beziehen (z.B. Leim, Schrauben, Nägel, etc).
Der Erfolg beim Erlernen von hochqualitativen Wortvektorisierungen hängt fast ausschließlich von der Qualität und der Menge an Lerndaten ab. Üblicherweise bestehen die Datensätze, die man benötigt, um einem Computer bestimmte Wissensbereiche beizubringen aus 107 – 1010 Wörtern. Ideale Trainingsdaten, um die feinen Details von Beziehungen zwischen Wörtern zu erlernen, sollten also so groß wie möglich sein und alle erdenklichen Kombinationen von Wörtern im Sprachgebrauch umfassen, aber möglichst wenige Redundanzen enthalten.
Visualisierung von semantischen Zusammenhängen zwischen Wörtern
Die Auswertung der Qualität von Sprachverständnis/-gestaltung ist per Definition sehr subjektiv. Es ist schwer, eine kalkulierbare Messgröße dafür zu bestimmen. Um sicherzustellen, dass Wortvektorisierungen sinnvoll sind, können Beziehungen zwischen Wörtern, aus denen sich der Datenbestand zusammensetzt, von einem Menschen untersucht und mit menschlichem Sprachverständnis verglichen werden. Dabei ist es zu erwarten, dass Wörter, die durch nah beieinanderliegende Vektoren ausgedrückt werden, auch von Menschen als sehr ähnlich eingeschätzt würden. Wortvektoren sind durch ihre Vieldimensionalität schwer vorstellbar, können aber durch bestimmte Techniken auf drei- oder zweidimensionale Darstellungen reduziert werden – z.B. principal component analysis (PCA) oder t-Distributed Stochastic Neighbor Embedding (t-SNE).
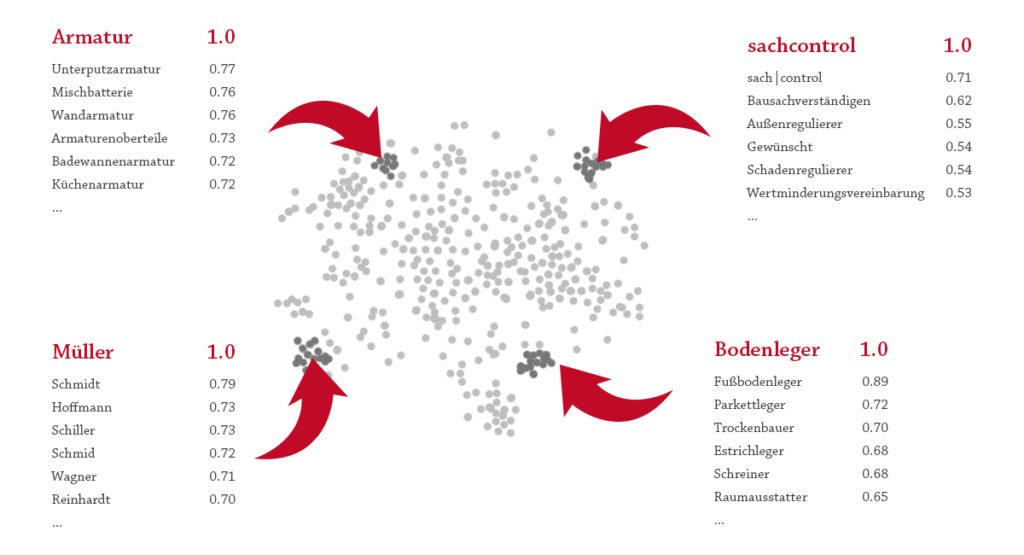
Bei sachcontrol setzen wir Datenmodelle zur Vektorisierung von Wörtern aus Handwerkerdokumenten ein. Es ist eine sehr spannende Übung, durch die Wörterwolken zu stöbern und darin eine überraschend menschlich anmutende Logik zu entdecken. Ein paar Beispiele: Alle Typen von „Armatur“ verdichten sich in einer kompakten Wolke, was hervorhebt, dass unser vektorisierender Computeralgorithmus gelernt hat, diese Wörter zu gruppieren, unabhängig davon, wie unterschiedlich sie geschrieben werden. Der Algorithmus folgt auch wunderbar der menschlichen Intuition, indem er sowohl Handwerkergruppen und typische deutsche Familiennamen gruppiert. Da in dem Datenbestand für den Lernprozess häufig das Wort sachcontrol auftaucht, hat der Computeralgorithmus auch die Vektorisierung von „sachcontrol“ gelernt. Wie zu erwarten war, weist der Unternehmensname enge Beziehungen zu den Begriffen anderer Angebote und deren Mehrwerte auf.
Mathe mit Worten
Die Möglichkeit, Wörter als Vektoren darzustellen, erlaubt es uns auch mathematische Operationen auf Wörter anzuwenden. Oder genauer gesagt auf die Konzepte, die sich hinter Wörtern verbergen. Zum Beispiel könnte man unter Verwendung von Wortvektoren semantische Fragen wie „Was ist ein König, der kein Mann, sondern eine Frau ist?“ beantworten. Solche Fragen können mathematisch wie folgt dargestellt werden: Wort1 – Wort2 + Wort3 = ?. Oder im Fall unserer Beispielfrage wäre es: König – Mann + Frau = Königin.
Um semantische Fragen mathematisch zu beantworten, werden zuerst alle Worte in Vektoren umgewandelt. Anschließend werden arithmetische Rechenoperationen vorgenommen, um den Ergebnisvektor zu ermitteln. Aus dem vorhandenen Vokabular werden die Wörter gewählt, deren Vektoren am dichtesten an dem errechneten Vektor liegen. Der am nächsten liegende Vektor hat dabei die höchste Wahrscheinlichkeit, die richtige Antwort auf die Frage zu sein. In den nachfolgenden Beispielen sind jeweils die drei wahrscheinlichsten Antworten und deren Ähnlichkeit zum Ergebnisvektor der Berechnung dargestellt.
-
Dank der Wort-Vektorisierung kann der Computer mathematische Operationen mit Wörtern ausführen.
-
Dazu führt die Maschine einfache Rechenoperationen mit den Vektoren der einzelnen Wörter aus…
-
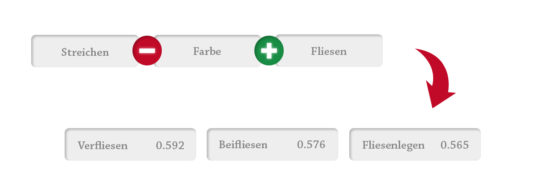
… und gibt die am nächsten liegenden Wort-Vektoren als Ergebnisse aus. Diese gelten als wahrscheinlichste richtige Antworten auf die gestellten Fragen..
Die Beispiele verdeutlichen, wie mathematische Berechnungen von semantischen Ähnlichkeiten bei Begriffen aus dem Handwerkerumfeld funktionieren. Sie zeigen, wie die Antworten zu Fragen hergeleitet werden: „Wie heißt das Zimmer, wenn beim Wohnzimmer Laminat entfernt und Fliesen hinzugefügt werden?“ oder „Wie nennt sich der Prozess des Malens ohne Farbe, aber mit Fliesen?“
Ziemlich beeindruckend. Durch einfache lineare Algebra sind wir in der Lage, die Bedeutung von Wörtern und deren Beziehungen zueinander zu ermitteln. Die Fähigkeit hat zwar zunächst erstmal keinen direkten praktischen Nutzen, es ist aber wichtig zu zeigen, dass unsere Wortvektorisierung erfolgreich die feinen Details der Sprache deutscher Handwerker gelernt hat.
Wortvektoren geschafft. Was kommt als nächstes?
Wörter sind grundlegende Bausteine der Sprache. Deren Umwandlung in maschinen-nutzbare Formate, Vektoren, ist der erste Schritt bei der Entwicklung künstlicher Intelligenz auf menschlichem Niveau, die fähig ist, komplexe Zusammenhänge in Handwerkerdokumenten zu verstehen. Wortvektoren enthalten grundsätzlich wertvolle semantische Informationen. Sie befähigen uns, komplexe Algorithmen so zu bauen und zu trainieren, dass Maschinen Handwerkerdokumente so verstehen können, wie sonst nur Menschen.
Bildquellen
- Vektor Hund-Katze-Stuhl: Bildrechte bei sachcontrol
- Grafik: Vektoren der Wörter: Bildrechte bei sachcontrol
- 2D-Darstellung von Wortvektoren: Bildrechte bei sachcontrol
- Grafik: Rohrbruch – Wasser + Dach: Bildrechte bei sachcontrol
- Grafik: Wohnzimmer – Laminat + Fliesen: Bildrechte bei sachcontrol
- Roboter löst Aufgaben an Tafel: Shutterstock - Phonlamai Photo
Tags In
Meistgelesene Posts
- Ein Blick hinter die Kulissen: Die Belegprüfung bei sachcontrolBelegprüfung – was ist das eigentlich? Diese Frage hat...
- Daher weht der Wind…Ob Friederike, Kyrill oder Xavier. Jeder hat sie schon...
- Top 5 – Die verrücktesten SchadenmeldungenRund 62.000 Schadensfälle werden in Deutschland laut GD...
- Warum feiern wir eigentlich Ostern?Die ersten warmen Sonnenstrahlen des Jahres lassen die...
- sachjournal im Gespräch – Solera und In4mo über den “Familienzuwachs” und optimierte Schadenprozesse (Teil 1)Vor einiger Zeit wurde In4mo von Solera gekauft. Um uns...